Sự Kết Hợp Tuyệt Vời Của Máy Tính và Phương Pháp Số
- Feb 29, 2020
- 4 min read
Updated: Dec 30, 2020
Chào các bạn,
Không phải một cái máy CASIO nhiều chức năng, không phải một cái máy Computer hay Laptop như bây giờ. Thời mình đi học phổ thông mua được cái máy tính CASIO là mừng lắm các bạn. Ngày nào cũng đi ngang cửa hàng bán sách cùng với thằng bạn thân tìm sách và nghía tới nghía lui cái máy CASIO fx 500MS mới ra. Thời đó, máy này là ước ao lớn của mình rồi các bạn. Vì so với máy fx 500A thì máy fx 500MS có phím ANS vi diệu.
Ví dụ đề bài cho công thức F(n) = F(n-1)x2 + 5 với F(0) = 5 và hỏi bạn F(5) bằng bao nhiêu? Bạn sẽ tính như thế nào?
F(0) = 5
F(1) = F(0)x2 + 5 = 15
F(2) = F(1)x2 + 5 = 35
F(3) = F(2)x2 + 5 = 75
F(4) = F(3)x2 + 5 = 155
F(5) = F(4)x2 + 5 = 315
Bạn sẽ bấm máy như thế nào:
Đầu tiên bạn bấm “5”, rồi bấm “=”
Sau đó, nhập biểu thức bằng cách bấm lần lượt ”Ans” “X” “2” “+” “5”
Màn hình máy tính sẽ như sau

Trên màn hình này, bạn cần biết “Ans” đang bằng “5” và nếu bấm “=” thì bạn sẽ nhận được F(1) = 15

Bấm tiếp “=” “=” “=” “=” (4 lần) bạn sẽ nhận được F(5) = 315
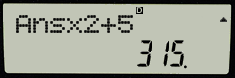
Oh, đơn giản quá, bấm tiếp 5 lần nữa xem nào

Và F(10) = 10235
Tuyệt vời, chúc mừng các bạn đã trải nghiệm phím “ANS” vi diệu trên máy CASIO fx 500 MS.
Mình có một bài toán khác dành cho bạn, tìm nghiệm x trong khoảng [3,4] của phương trình f(x) = x3– 3x2 – 5 = 0.
Ở thời điểm này, có thể bạn có nhiều cách tốt hơn để giải, nhưng ở bài viết này mình sẽ trình bày cách giải theo phương pháp lặp và tìm nghiệm gần đúng.
Đầu tiên, bạn đưa phương trình về dạng x = g(x) bằng cách chia 2 vế của phương trình cho x2 và biến đổi về dạng x= 3 + 5/x2. Ban đầu ta giả sử nghiệm gần đúng là 3.5 và xây dựng biểu thức lặp:
x0 = 3.5
xn = 3 + 5/(xn-1)2
Các bạn sẽ nhận được kết quả như sau:
x0 = 3.5
x1 = 3 + 5/(x0)2= 3.408163265
x2 = 3 + 5/(x1)2= 3.430456452
x3 = 3 + 5/(x2)2= 3.424879897
x4 = 3 + 5/(x3)2= 3.426264644
Trình tự bấm máy như sau,
Đầu tiên nhập “3.5” bấm “=”
Sau đó, bấm lần lượt, “3” “+” “5” “÷” “Ans” “x2”
Màn hình sẽ như sau:

Bấm “=” “=” “=” “=”“=” “=” (6 lần),

sau mỗi lần bấm bạn ghi lại kết quả vào bảng và tính được sai số sau mỗi bước lặp như sau:

Các bạn có thể nhìn thấy sau mỗi bước lặp, sai số giảm dần và ta có thể đưa ra dự đoán là bài toán có khả năng hội tụ về nghiệm chính xác. Nếu chấp nhận nghiệm gần đúng với sai số 0.001 bạn có thể dừng quá trình lặp và nhận được nghiệm gần đúng ở bước lặp thứ 5 là x = x5 = 3.425920158 ≈ 3.426. Nếu muốn nhận được nghiệm chính xác đến 0.0001 bạn hãy dừng ở bước lặp thứ 6 và nhận được nghiệm gần đúng x = x6= 3.426005817 ≈ 3.4260
Đối với ví dụ trên, bạn có thể tìm được nghiệm chính xác bằng phương pháp giải tích, nhưng có những phương trình bạn không thể và không bao giờ tìm được nghiệm chính xác. Các bạn còn nhớ có những bài tích phân không tìm được lời giải.
Giải phương trình và tìm nghiệm chính xác là công việc của các nhà toán học và họ luôn luôn nhận được thử thách đó từ các nhà nghiên cứu ở các lĩnh vực khác như cơ học, vật lý, xây dựng, cơ khí, hàng không, vận tải …
Trong thực tế và trong kỹ thuật, tùy vào từng đối tượng, từng lĩnh vực người ta luôn luôn chấp nhận một sai số nhất định và vì vậy các phương pháp tính, hay còn gọi là phương pháp số đã được nghiên cứu.
Các bạn đã từng biết đến:
- Phương pháp chia đôi
- Phương pháp lặp đơn (ví dụ ở trên)
- Phương pháp dây cung
- Phương pháp Newton
Và còn nhiều phương pháp số khác để giải nhiều dạng phương trình khác nhau như:
- Phương trình 1 ẩn f(x) = 0
- Hệ phương trình đại số tuyến tính
- Phương trình vi phân đạo hàm riêng
Việc tìm ra các mô hình toán học cho các bài toán thực tế là thách thức đối với các nhà nghiên cứu.
Ngày nay, máy tính là công cụ tuyệt vời để áp dụng các phương pháp số vào việc tìm ra lời giải và mô phỏng số cho các bài toán kỹ thuật ở hầu hết các lĩnh vực.

Các bạn đã từng biết đến Phương pháp phần tử hữu hạn? Đã từng nghe đến ANSYS, ABAQUS lừng danh? Hãy đừng lướt qua nó! Hãy tiếp tục, hãy luôn đặt câu hỏi và tìm câu trả lời. Tôi muốn nghe cảm giác bạn khi làm được điều gì đó và hét lên trong sự vui sướng.
Chúc các bạn thành công! Và hẹn gặp lại các bạn vào thứ bảy tuần tiếp theo nhé!




Comments